![next]()
![up]()
![previous]()
Next:
About this document ...
MATH69.217* ANSWERS TO
TEST 3 Fall 2001
- 1.
- (a) State the definition of an orthonormal basis in
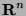 . (b) Verify the identity
. (b) Verify the identity
where  stands for the dot product of vectors
stands for the dot product of vectors 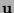 and
and  in
in 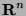 .
.
- Answer:
- (a) An orthonormal basis in
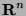 is a basis in
is a basis in
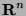 consisting of unit vectors perpendicular to each other.
(b) We begin with the right hand side:
consisting of unit vectors perpendicular to each other.
(b) We begin with the right hand side:
Done.
- 2.
- Find the entries
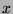 ,
,  and
and 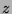 in the following orthogonal matrix
in the following orthogonal matrix
- Answer:
- From the fact that the first two columns are perpendicular, we obtain
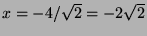 . From the fact that the first and the last rows are
perpendicular, we get
. From the fact that the first and the last rows are
perpendicular, we get 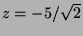 . Finally,
from the fact last two rows are perpendicular, we get
. Finally,
from the fact last two rows are perpendicular, we get 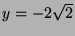 .
.
- 3.
- Find the projection of the vector
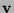 onto the
subspace spanned by the vectors
onto the
subspace spanned by the vectors  and
and  , where
, where
Begin by checking that 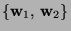 is an orthogonal system.
is an orthogonal system.
- Answer:
- First we check
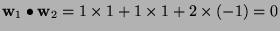 . Hence
. Hence 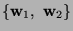 is indeed and orthogonal system. The required
projection is
is indeed and orthogonal system. The required
projection is
- 4.
- Find the QR factorization of the matrix
- Answer:
- Write
 ,
, 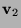 and
and 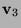 for the columns of
for the columns of  . Put
. Put 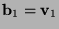 . Let
. Let
and
Upon normalization, we get an ONB:
The 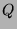 matrix in the
matrix in the 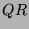 -decomposition
of
-decomposition
of  is
is
and the 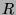 matrix is
matrix is



Next: About this document ...
C.K. Fong 2001-11-09 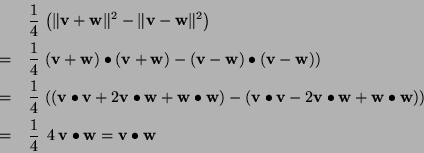
![\begin{displaymath}A={1\over 5}\, \left[\begin{array}{ccc}
4 & 3/\sqrt{2} & 3/\...
...{2} \\
3 & x & y \\
0 & 5/\sqrt{2} & z \end{array}\right]. \end{displaymath}](Old Test 3_files/img10.png)
![\begin{displaymath}{\bf v}=\left[\begin{array}{r} 3 \\ 2 \\ 2 \end{array}\right]...
...f w}_2=\left[\begin{array}{r} 1 \\ 1 \\ -1 \end{array}\right]. \end{displaymath}](Old Test 3_files/img17.png)
![\begin{displaymath}
\frac{{\bf v}\bullet{\bf w}_1}{{\bf v}\bullet{\bf w}_1}\ {\...
...
=\left[\begin{array}{r} 5/2 \\ 5/2 \\ 2 \end{array}\right]. \end{displaymath}](Old Test 3_files/img21.png)
![\begin{displaymath}A=\left[\begin{array}{ccc}
1 & 4 & 5 \\
2 & 2 & 1 \\
2 & 5 & 1 \end{array}\right] \end{displaymath}](Old Test 3_files/img22.png)
![\begin{displaymath}{\bf b}_2={\bf v}_2-
\frac{{\bf v}_2\bullet {\bf b}_1}{{\bf ...
...ght]
=\left[\begin{array}{r} 2 \\ -2 \\ 1 \end{array}\right], \end{displaymath}](Old Test 3_files/img28.png)
![\begin{eqnarray*}{\bf b}_3
&=&{\bf v}_3
-\frac{{\bf v}_3\bullet{\bf b}_1}{{\b...
...right]=
\left[\begin{array}{r}2 \\ 1 \\ -2 \end{array}\right]. \end{eqnarray*}](Old Test 3_files/img29.png)
![\begin{displaymath}{\bf u}_1=\frac{{\bf b}_1}{\Vert{\bf b}_1\Vert}
=\left[\begi...
...=\left[\begin{array}{r} 2/3 \\ 1/3 \\ -2/3 \end{array}\right]. \end{displaymath}](Old Test 3_files/img30.png)
![\begin{displaymath}Q=\left[\begin{array}{rrr}
1/3 & 2/3 & 2/3 \\
2/3 &-2/3 & 1/3 \\
2/3 & 1/3 &-2/3 \end{array}\right] \end{displaymath}](Old Test 3_files/img33.png)
![\begin{displaymath}R=Q^\top A=\left[\begin{array}{rrr}
1/3 & 2/3 & 2/3 \\
2/3...
...}
3 & 6 & 3 \\
0 & 3 & 3 \\
0 & 0 & 3 \end{array}\right]. \end{displaymath}](Old Test 3_files/img35.png)
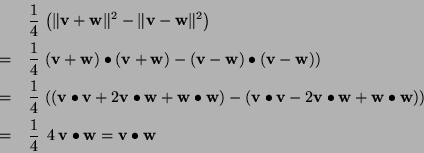
![\begin{displaymath}A={1\over 5}\, \left[\begin{array}{ccc}
4 & 3/\sqrt{2} & 3/\...
...{2} \\
3 & x & y \\
0 & 5/\sqrt{2} & z \end{array}\right]. \end{displaymath}](Old Test 3_files/img10.png)
![\begin{displaymath}{\bf v}=\left[\begin{array}{r} 3 \\ 2 \\ 2 \end{array}\right]...
...f w}_2=\left[\begin{array}{r} 1 \\ 1 \\ -1 \end{array}\right]. \end{displaymath}](Old Test 3_files/img17.png)
![\begin{displaymath}
\frac{{\bf v}\bullet{\bf w}_1}{{\bf v}\bullet{\bf w}_1}\ {\...
...
=\left[\begin{array}{r} 5/2 \\ 5/2 \\ 2 \end{array}\right]. \end{displaymath}](Old Test 3_files/img21.png)
![\begin{displaymath}A=\left[\begin{array}{ccc}
1 & 4 & 5 \\
2 & 2 & 1 \\
2 & 5 & 1 \end{array}\right] \end{displaymath}](Old Test 3_files/img22.png)
![\begin{displaymath}{\bf b}_2={\bf v}_2-
\frac{{\bf v}_2\bullet {\bf b}_1}{{\bf ...
...ght]
=\left[\begin{array}{r} 2 \\ -2 \\ 1 \end{array}\right], \end{displaymath}](Old Test 3_files/img28.png)
![\begin{eqnarray*}{\bf b}_3
&=&{\bf v}_3
-\frac{{\bf v}_3\bullet{\bf b}_1}{{\b...
...right]=
\left[\begin{array}{r}2 \\ 1 \\ -2 \end{array}\right]. \end{eqnarray*}](Old Test 3_files/img29.png)
![\begin{displaymath}{\bf u}_1=\frac{{\bf b}_1}{\Vert{\bf b}_1\Vert}
=\left[\begi...
...=\left[\begin{array}{r} 2/3 \\ 1/3 \\ -2/3 \end{array}\right]. \end{displaymath}](Old Test 3_files/img30.png)
![\begin{displaymath}Q=\left[\begin{array}{rrr}
1/3 & 2/3 & 2/3 \\
2/3 &-2/3 & 1/3 \\
2/3 & 1/3 &-2/3 \end{array}\right] \end{displaymath}](Old Test 3_files/img33.png)
![\begin{displaymath}R=Q^\top A=\left[\begin{array}{rrr}
1/3 & 2/3 & 2/3 \\
2/3...
...}
3 & 6 & 3 \\
0 & 3 & 3 \\
0 & 0 & 3 \end{array}\right]. \end{displaymath}](Old Test 3_files/img35.png)